

Click on the author name to see the abstract.
| Chair: Fabian Pauly | |
| 09:30-10:05 | Bezanilla |
| 10:05-10:30 | Achilli |
| 10:30-11:00 | Coffee break |
| Chair: Jian-Sheng Wang | |
| 11:00-11:35 | Delgado |
| 11:35-12:10 | Donarini |
| 12:10-12:35 | Minamitani |
| 12:35-13:00 | Droghetti |
| 13:00-13:10 | Closing remarks |
Invited talk
Quantum transport properties across different chemical decorations in layered materials
Argonne National Laboratory, Lemont, Illinois 60439, USA
New materials with greater capabilities are a key component in the strategy to further the performance of current electronic devices. Of the limited available base options, light element layered materials are among the most promising solutions for high-performance charge transport with low heat dissipation. But the small or the absence of an electronic band gap in materials such as graphene prevents the creation of an on-to-off switch, hindering their integration in today's electronics. Within this setting, and motivated by prospects of integrating layered compounds into electronic devices to reduce consumer power consumption, I will describe how various types of chemical modifications and structural disorder in bilayer graphene [1], double-walled nanotubes [2] , as well as some new 2D materials such as black phosphorus [3] and silicene [4] can enlarge the small or non-existing electronic band gaps while preserving a good charge mobility. I will discuss the required chemistry criteria for each material, which are obtained using a combination of electronic-structure and quantum transport computational methods at the micro-meter scale, to select the type of external defect and stoichiometry for achieving specific transport profiles.
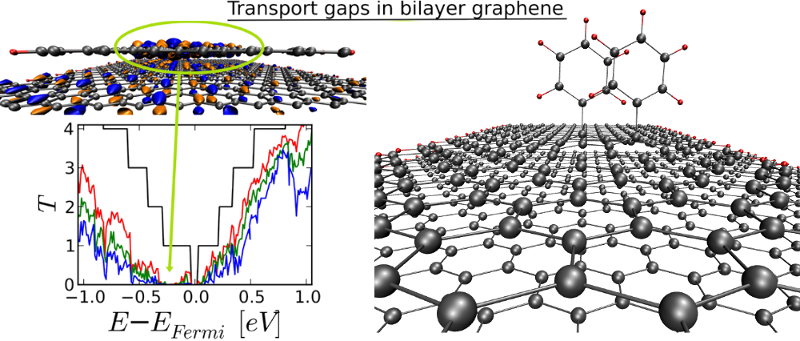
Figure 1: Defected bilayer graphene yields homogeneous transport profiles across different chemical modifications.
[1] A.Lopez-Bezanilla, J. Phys. Chem. C 118, 29467 (2014).
[2] A.Lopez-Bezanilla, J. Phys. Chem. C 118, 1472 (2014).
[3] A.Lopez-Bezanilla, Phys. Rev. B 93, 035433 (2016).
[4] A.Lopez-Bezanilla, Phys. Chem. C 118, 18788 (2014).
Contributed talk
First principle semiclassical conductivity and quantum transport in graphene with resonant scatterers: the case of H and F adatoms and of carbon atom vacancies
1Dipartimento di Chimica, Università degli Studi di Milano, v. Golgi 19, 20133 Milano, Italy
2Dipartimento di Fisica, Università Cattolica del Sacro Cuore, v. dei Musei 41, 25121 Brescia, Italy
3CNR-ISTM Istituto di Scienze e Tecnologie Molecolari, v. Golgi 19, 20133 Milan, Italy
The outstanding electronic and mechanical properties of graphene are unavoidably affected by the presence of a variety of possible defects in realistic samples. Atomic-scale defects such as charge scatterers, adatoms and carbon atom vacancies are typically introduced during the fabrication process and largely impact on its charge and spin transport properties. In this context neutral impurities which form resonant scattering centers have attracted much attention in the last few years, and considered to be important scatterers limiting electronic mobility [1,2].
Here, we analyze the effect of neutral defects on the transport properties of graphene, evaluating from first principles the cross section of resonant scatterers like H and F adatoms, and single C atom vacancies. The conductivity of two dimensional graphene with the above neutral impurities is calculated in the semi-classical limit where coherence is assumed to be lost between two scattering events, using a DFT-NEGF approach [3,4] on several defective graphene channels of different width and length. Quantum transport at and close to the Dirac point is further analyzed, and the same universal behavior is proved to exist for the intrinsic resistance of the defective transport channels, irrespective of the scatterer considered.
[1] N. M. R. Peres, J. Phys: Condens. Matter 21, 323201 (2009).
[2] S. Das Sarma, S. Adam, E. H. Hwang, and E. Rossi, Rev. Mod. Phys. 83, 407 (2011).
[3] J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón, and D. Sánchez-Portal, J. Phys.: Condens. Matter 14, 2745 (2002).
[4] M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor, K. Stokbro, Phys. Rev. B 65, 165401 (2002).
Invited talk
Modeling magnetism of single molecules: from electronic structure to spin-flip spectroscopy
1Centro de Física de Materiales CSIC-UPV/EHU; Donostia International Physics Center (DIPC), Departamento de Física de Materiales UPV/EHU, Paseo Manuel de Lardizabal 5, 20018 Donostia-San Sebastián, Spain
2IKERBASQUE, Basque Foundation for Science, 48013 Bilbao, Spain
3Instituto de Física, Universidad Autónomade San Luis Potosí 68000, San Luis Potosí, México
4Departamento de Física Aplicada, Universidad de Alicante, San Vicente del Raspeig s/n 03690, Alicante, Spain
Magnetic molecules and single-molecule magnets in particular have attracted a lot of interest due to their capability to store magnetic information, offering a high storage density, promising stability and fast spin-manipulation [1]. Information about the magnetic properties of ensembles of these molecules is available through a series of experimental techniques, from variable-temperature magnetic susceptibility, to infrared spectroscopy, neutron scattering or electron paramagnetic resonance [2]. In addition, spin-flip spectroscopy provides a direct access to spectroscopic information of single molecules deposited on a substrate [3]. Density functional theory (DFT) calculations yields valuable theoretical information of these objects, but it is not especially suited to treat the low-energy magnetic properties. By contrast, spin models offer detailed information of the magnetic properties which can be directed compared with experiments, but they lack of the predictive capability of DFT since they rely on phenomenological parameters. Here we show that by combining DFT and electronic or spin models one can extract magnetic properties such as the magnetic susceptibility. We illustrate the treatment with Co-benzene magnetic clusters where we predict a non-collinear magnetization [4]. In addition, we show that the transport properties can very often be studied by using a generalized Anderson model. In particular, we demonstrate that cotunneling is the leading mechanism that accounts for the spin-assisted inelastic conductance observed in adsorbed Co-phthalocyanine molecules [5].
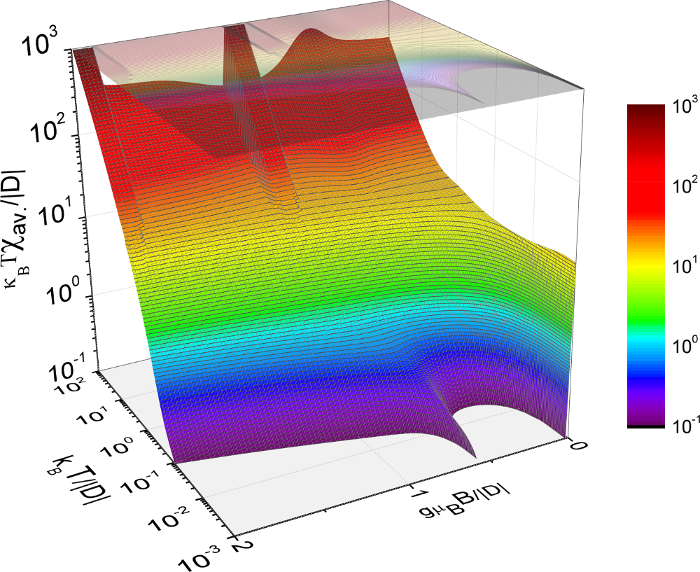
Figure 1: Contour plot of the average magnetic susceptibility of a (CoBc)3 molecule versus applied magnetic field and temperature (in units of the uniaxial magnetic anisotropy parameter D).
[1] M. N. Leuenberger and D. Loss, Nature 410, 789 (2001).
[2] A. Furrer and O. Waldmann, Rev. Mod. Phys. 85, 367 (2013).
[3] X. Chen et al., Phys. Rev. Lett. 101, 197208 (2008).
[4] A. W. González et al., in preparation.
[5] F. Delgado and J. Fernández-Rossier, Phys. Rev. B 84, 045439 (2011).
Invited talk
Many-body correlations in STM single molecule junctions
Institute of Theoretical Physics, University of Regensburg, 93040 Regensburg (Germany)
The electronic structure and the transport characteristics of single molecule junctions are strongly influenced by many-body correlations. Some of their fingerprints have been theoretically predicted [1,2] others clearly observed in STM experiments [3,4] both at the spectral and topographical level. We consider here a copper phthalocyanine (CuPc) molecule on an insulator coated substrate and demonstrate the non-equilibrium tip induced control of the molecular spin state. We find that, under the condition of energetic proximity of many-body neutral excited states to the anionic ground state, the system can undergo a population inversion towards these excited states. The resulting state of the system is accompanied by a change in the total spin quantum number [5]. Experimental signatures of the crossover are the appearance of additional nodal planes in the topographical STM images as well as a strong suppression of the current near the center of the molecule. The robustness of the effect against moderate charge conserving relaxation processes has also been tested.
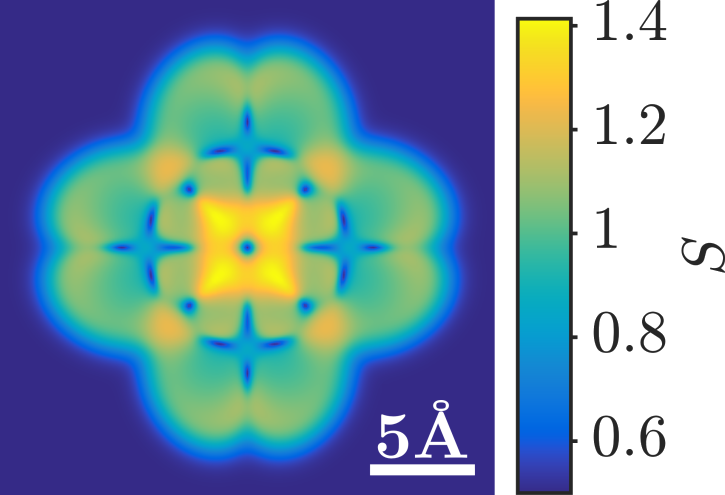
Figure 1: Simulation of the spin map of a Cu-Phthalocyanine as a function of tip position. At specific tip positions a low to high spin transition on the molecule is triggered by the external bias across the junction and is accompanied by population inversion towards excited molecular states.
[1] A. Donarini, G. Begemann, and M. Grifoni Nano Lett. 9, 2897 (2009).
[2] D. Toroz, M. Rontani and S. Corni, Phys. Rev. Lett. 110, 018305 (2013).
[3] F. Schulz, M. Ijäs, R. Drost, S. K. Hämäläinen, A. Harju, A. P.Seitsonen, and P. Liljeroth, Nat. Phys. 11, 229 (2015).
[4] B. W. Heinrich, L. Braun, J. I. Pascual, and K. J. Franke, Nat. Phys. 9, 765 (2013).
[5] B. Siegert, A. Donarini, and M. Grifoni, Phys.Rev. B 93, 121406(R) (2016).
Contributed talk
Tunable competition between Kondo effect and spin-orbit interaction in a single molecule
1Department of Materials Engineering, The University of Tokyo, Japan
2Department of Advanced Materials Science, The University of Tokyo, Japan
3International Center for Materials Nanoarchitectonics (WPI-MANA), National Institute for Materials Science, Japan
The Kondo effect and the spin-orbit interaction (SOI) play important roles to determine the magnetism of a single molecule. On metallic substrate, the local magnetic moment of a molecule is screened by the substrate conduction electron, which gives rise to a sharp peak (Kondo resonance) at the Fermi level in the differential conductance (dI/dV). The SOI splits the degenerate states with spin magnetic quantum number Sz into multiple fine structures (SO splitting), which causes magnetic anisotropy. The competition between the Kondo effect and the SO splitting results in exotic physics [1], but is not sufficiently understood yet.
In this study, we investigate the above competition, focusing on iron phthalocyanine (FePc) on Au(111). Bulk FePc molecules take S=1 triplet state consists of the unpaired electrons in Fe dz2 and degenerate dzx/dyz orbitals. The SO splitting induces the in-plane magnetic anisotropy and energy gap opens between Sz=0 and Sz=±1, which suppresses the Kondo resonance. On the contrary, a clear Kondo resonance appears in the dI/dV spectrum measured by scanning tunneling spectroscopy (STM) in FePc/Au(111) [2,3]. We modeled this system by an extended two-orbital and two-channel Kondo model and analyzed by using the numerical renormalization group technique [4]. We found that the strong renormalization of the SO splitting by two-channel Kondo screening enables to form the Kondo resonance. With reducing the Kondo coupling, the Kondo resonance formation is hampered by the SO splitting and the gap structure in the dI/dV spectrum develops instead of the Kondo resonance peak structure. The reduction of the Kondo coupling can be achieved by changing the Fe atom position. We realized this by STM experiments [4]. As the STM tip approaches to the Fe ion in FePc/Au(111), the spectral shape and the width of the dip in the dI/dV spectrum is changed, which is rationalized by the transition from the Kondo-effect-dominant state to the SO-splitting-dominant state.
[1] J. J. Parks et al., Science 328, 1370-1373 (2010).
[2] N. Tsukahara et al., Phys. Rev. Lett. 106, 187201 (2011).
[3] E. Minamitani et al., Phys. Rev. Lett. 109, 086602 (2012).
[4] R. Hiraoka et al., submitted.
Contributed talk
Electron transport simulations in the Kondo regime
1Universidad del Pais Vasco, Spain
2University of Augsburg, Germany
3National Physical Laboratory, UK
When magnetic atoms and molecules are brought into contact with metals the electron-electron interaction leads to the appearance of the correlated Kondo state at low temperatures. In this talk we will outline the methodological approach to evaluate the conductance of such systems from first principles, which is implemented in the Smeagol electron transport code [1]. In particular, we integrate the Density Functional Theory (DFT) with the continuous time quantum Monte Carlo (CTQMC) and the Numerical Renormalization Group (NRG) impurity solvers. We will present results of simulations for STM and break junction experiments that investigated stable radical molecules [2,3]. These molecules correspond to spin half molecular magnets. Finally we will briefly mention how the method has been extended to treat solid state devices, such as metallic heterostructures, within the Dynamical Mean Field Theory (DMFT) [4].
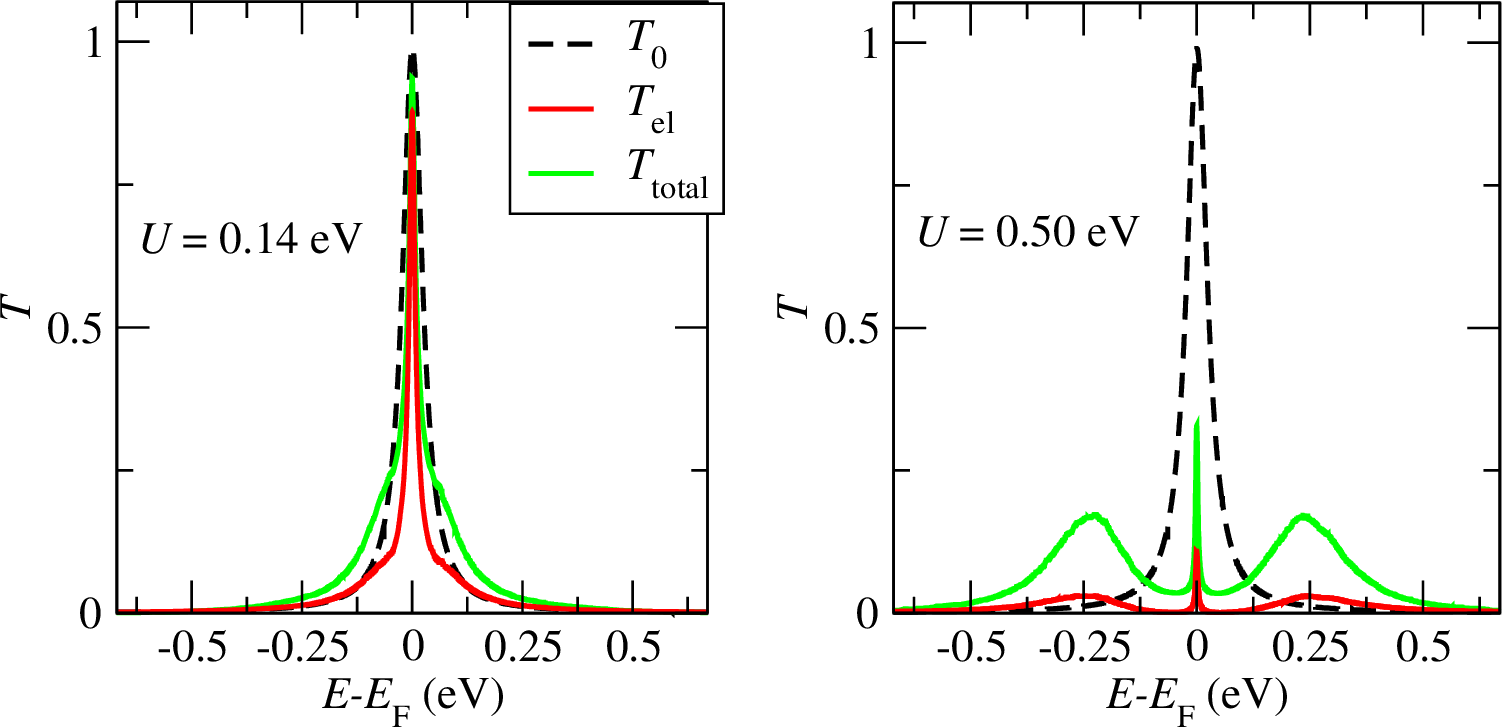
Figure 1: DFT transmission function (T0) compared to the DFT+CTQMC coherent (Te) and total, i.e. coherent+incoherent (Ttotal) transmission function for a spin ½ magnetic molecule between gold electrodes.
[1] A. Rocha et al., Nature Mater. 4, 335 (2005), A. Rocha et al., Phys. Rev. B 73, 085414 (2006), I. Rungger et al., Phys. Rev. B 78, 035407 (2008).
[2] J. Liu et al., J. Am. Chem. Soc. 135, 651 (2013).
[3] R. Frisenda et al., Nano Lett. 15, 3109 (2015).
[4] L. Chioncel et al., Phys. Rev. B 92, 054431 (2015).